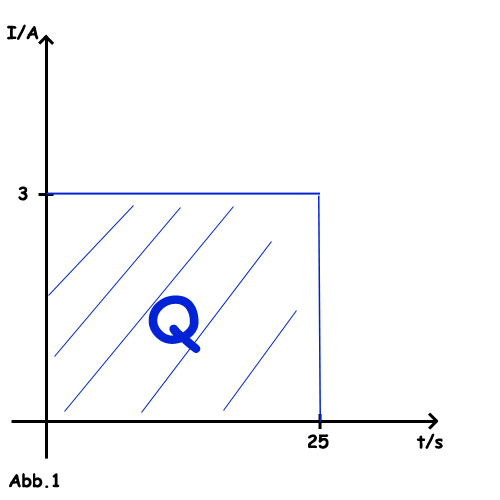
In Abbildung 1 ist die Stromstärke in Abhängigkeit von der Zeit bei einer konstanten Stromsträke gezeigt. Die Fläche unter dem Graphen bezeichnet die Ladung. Es ist zu erkennen, dass sich bei einer konstanten Stromstärke die Ladung sehr einfach ermitteln lässt. Es gilt:

Q(t) = I*t (nur für I = konstant)
Am Beispiel der Abb.1, I = 3 Ampere und t = 25 Sekunden:
Q(25s) = 3A * 25s = 75As = 75 C (Coulomb)

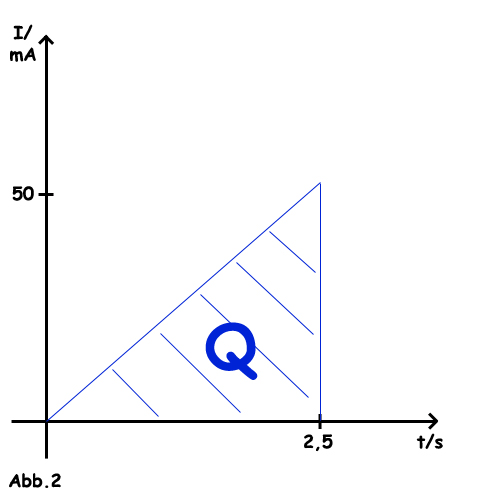
In der nächsten Abbildung ist ein anderer Sachverhalt gezeigt, die Stromstärke steigt linear an. Auch hier wird die Ladung durch die Fläche unter dem Graphen beschrieben. Diesmal müssen wir aber kein Rechteck wie in Abb.1, sondern den Flächeninhalt eines Dreiecks berechnen. Als allgemein Formel dafür gilt: A = 1/2*Grundseite*Höhe! Übertragen auf unsere Situation ergibt sich folgendes:

Q(t) = 1/2*I*t
Auch hier rechnen wir wieder mit den Zahlen aus dem Diagramm:
Q(2,5s) = 1/2*2,5s*50mA = 62,5mA = 62,5mC = 0,0625 C

In der Abbildung drei wird uns eine Stromstärke-Zeit-Funktion gezeigt, die quadratisch zunimmt. Auch bei einer quadratischen Funktion wir die Ladung zwar durch die Fläche unter dem Graphen beschrieben, allerdings ist die Rechnung etwas komplizierter. Durch die Bildung eines Integrals - Umgekehrtes Verfahrung der Ableitungsbildung - lässt sich die geflossene Ladung für einen Intervall berechnen. So kann man hinterher zum Beispiel genaue Aussagen über den Ladungsfluß zwischen der fünften und siebten Sekunde treffen. Hierzu benötigen wir allerdings zuerst die Funktion der Parabel.
Diese geben wir zunächst vor: I(t) = 1,5A*t²/s²

\[\text{Bildung eines Integrals:}\] \begin{align*} I(t)&=1,5 \cdot A\cdot \frac{t^2}{s^2}\\ Q(t)&= \int I(t)\;dt\\ &=\int\left(1,5\cdot A\cdot \frac{t^2}{s^2}\right)dt \end{align*} \[\text{Der Exponent wird nun um 1 erhöht und durch den vorderen Wert geteilt!}\] \begin{align*} Q(t)&=\int_{\text{untere Grenze}}^{\text{obere Grenze}}\left(\frac{1}{2}\cdot A\cdot \frac{t^2}{s^2}\right)\; dt\\\\ Q(t)&=\int^{7}_{5}\left[\left(\frac{1}{2}\cdot A\cdot \frac{7^2}{s^2}\right)-\left(\frac{1}{2}\cdot A\cdot \frac{5^2}{s^2}\right)\right]\;dt\\\\ &=171,5As-62,5As=109As=109mC \end{align*}